1128. Проблема Лонги
Лонги хорошо
разбирается в математике, он любит задумываться над трудными математическими
задачами, которые могут быть решены при помощи некоторых изящных алгоритмов. И
вот такая задачка возникла:
Дано целое число
n. Вычислите ∑gcd(i, n)
для всех 1 ≤ i ≤ n.
“О, я знаю, я
знаю!” – воскликнул Лонги! А знаете ли Вы? Пожалуйста, решите её.
Вход. Каждая строка содержит одно число n (1 < n < 231).
Выход. Для каждого
значения n выведите в отдельной
строке сумму ∑gcd(i, n) для всех 1 ≤ i ≤ n.
|
Пример
входа |
Пример
выхода |
|
2 6 12 |
3 15 40 |
РЕШЕНИЕ
теория
чисел
Анализ алгоритма
Теорема. Если функция f(n) мультипликативна, то
сумматорная функция Sf(n) = ![]() также
мультипликативна.
также
мультипликативна.
► Пусть x, y
Î N, причем x и y
взаимно просты. Пусть x1, x2, …, xk – все делители x.
Пусть y1, y2, …, ym – все делители y.
Тогда НОД(xi, yj) = 1, а все возможные
произведения xiyj
задают все делители xy. Тогда
Sf (x) * Sf (y) =  *
*  =
= ![]() =
= ![]() = Sf (xy)
= Sf (xy)
Следствие. Рассмотрим функцию f(n) = НОД(n, c), где c – константа. Если x и y взаимно просты, то
f(x * y) = НОД(x * y, c)
= НОД(x, c) * НОД(y, c) = f(x) * f(y). Следовательно
функция f(n) = НОД(n, c)
мультипликативна.
Пусть g(n) =  . Тогда
. Тогда
g(![]() ) = g(
) = g(![]() ) * g(
) * g(![]() ) * … * g(
) * … * g(![]() )
)
Теорема. Для любого простого p и натурального a имеет место соотношение:
g(pa) = (a + 1)pa – apa–1
► При а = 1 имеем:
g(p) = НОД(1, p) + НОД(2, p) + … + НОД(p, p)
= (p – 1) + p = 2p – 1
Аналогично при а = 2:
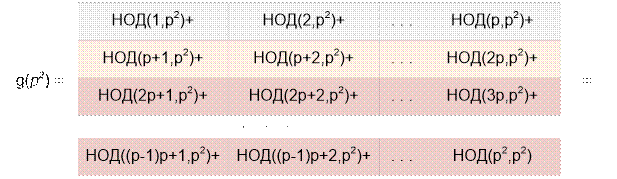
= (1 + 1 + … + 1 +
p) +
(1 + 1 + … + 1 +
p) +
…
(1 + 1 + … + 1 +
p2) =
= (p – 1 + p) * (p – 1) + (p – 1 + p2) =
(2p – 1) * (p – 1) + (p2 + p – 1) =
2p2 – 2p – p + 1 + (p2 + p – 1) =
= 3p2 – 2p
Лемма. Если d –
делитель n, то существует в точности ![]() таких чисел i что
НОД(i, n) = d.
таких чисел i что
НОД(i, n) = d.
► Очевидно
что i должно делиться на d, пусть i = dj. Тогда
НОД(i, n)
= НОД(dj, n) = d * НОД(j, n
/ d)
Если последнее
выражение равно d, то НОД(j, n
/ d) = 1. Количество таких j что НОД(j, n / d) = 1 равно ![]() .
.
Пример. Количество таких чисел i что НОД(i, 24) = 3 равно ![]() = 4.
= 4.
НОД(j, 8) = 1 при j Î {1, 3, 5, 7}, следовательно НОД(i, 24) = 3 при i Î {3, 9, 15, 21}
(у нас i = 3j).
Теорема.
g(n) =  =
= 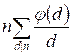
► Согласно
выше приведенной лемме количество пар (i,
n), для которых НОД(i, n)
= e, имеется в точности ![]() . Положив n / e = d, получим:
. Положив n / e = d, получим:
g(n) =  =
=  =
= 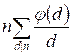
Пример. Пусть n = 6.

Тогда g(6) =  =
=
= НОД(1, 6) +
НОД(2, 6) + НОД(3, 6) + НОД(4, 6) + НОД(5, 6) + НОД(6, 6) =
= 1 + 2 + 3 + 2
+ 1 + 6 = 15
В то же время
g(6) = g(2) * g(3) =
(НОД(1, 2) +
НОД(2, 2)) * (НОД(1, 3) + НОД(2, 3) + НОД(3, 3)) =
(1 + 2) * (1 + 1
+ 3) = 3 * 5 = 15
Вычислим g(6) по
формуле g(n) = 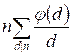 :
:
g(6) = =
=  =
=
= ![]() = 6 + 3 + 4 + 2 = 15
= 6 + 3 + 4 + 2 = 15
Вычислим g(6)
исходя из мультипликативности функции f(x)
= НОД(x, n):
g(6) = g(2) * g(3)
= (2*2 – 1) * (2*3 – 1) = 3 * 5 = 15
Пример. Пусть n = 12. Тогда g(12) =  =
=
1 + 2 + 3 + 4 +
1 + 6 + 1 + 4 + 3 + 2 + 1 + 12 = 40

В то же время g(12)
= g(4) * g(3) =
(НОД(1, 4) +
НОД(2, 4) + НОД(3, 4) + НОД(4, 4)) *
* (НОД(1, 3) +
НОД(2, 3) + НОД(3, 3)) =
(1 + 2 + 1 + 4)
* (1 + 1 + 3) = 8 * 5 = 40
Вычислим g(12)
по формуле g(n) = 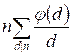 :
:
g(12) = =
=  =
=
= ![]() =
=
= 12 + 6 + 8 + 6
+ 4 + 4 = 40
Делителями числа
12 являются: 1, 2, 3, 4, 6, 12. Количество таких i что НОД(i, 12) = d равно ![]() . Например НОД(i,
12) = 3 имеет место для
. Например НОД(i,
12) = 3 имеет место для ![]() =
= ![]() = 2 различных i, а именно для i = 3, 9.
= 2 различных i, а именно для i = 3, 9.
Вычислим g(12)
исходя из мультипликативности функции f(x)
= НОД(x, n):
g(12) = g(22)
* g(3) = (3 * 22 – 2 * 2) * (2*3 – 1) = 8 * 5 = 40
Реализация алгоритма
Функция euler вычисляет функцию Эйлера.
long long euler(long long n)
{
long long i, result = n;
for (i = 2; i * i <= n;i++)
{
if (n % i == 0) result -= result / i;
while (n % i == 0) n /= i;
}
if (n > 1) result -= result / n;
return result;
}
Основная часть
программы. Читаем значение n. Вычислим
значение g(n) по формуле  . Все делители n
ищем среди чисел от 1 до
. Все делители n
ищем среди чисел от 1 до ![]() . Если i – делитель
n, то n / i также будет
делителем n. Поэтому с каждым
найденным делителем i ≤
. Если i – делитель
n, то n / i также будет
делителем n. Поэтому с каждым
найденным делителем i ≤ ![]() к результату res следует прибавить
к результату res следует прибавить  . Если n является
полным квадратом, а i = sq =
. Если n является
полным квадратом, а i = sq = ![]() , то
, то  и в сумму res добавится два одинаковых слагаемых.
Поэтому одно из них вычтем из res еще
на этапе инициализации этой переменной.
и в сумму res добавится два одинаковых слагаемых.
Поэтому одно из них вычтем из res еще
на этапе инициализации этой переменной.
while(scanf("%lld",&n)
== 1)
{
sq = (long long)sqrt(1.0*n);
res = (sq * sq == n) ? -sq * euler(sq) : 0;
for(i = 1; i
<= sq; i++)
if(n % i ==
0) res = res + i * euler(n/i) + (n / i) * euler(i);
printf("%lld\n",res);
}
Реализация с учетом мультипликативности
#include <stdio.h>
#include <math.h>
long long i, n, res, a, p;
int main(void)
{
while(scanf("%lld",&n)
== 1)
{
res = 1;
for(i = 2; i * i <= n; i++)
{
if(n % i == 0)
{
a = 0; p = 1;
while(n % i == 0)
{
a++;
p *= i;
n /= i;
}
res *= (a + 1)
* p - a * p / i;
}
}
if (n > 1) res *= (2*n - 1);
printf("%lld\n",res);
}
return 0;
}
Java реализация
import
java.util.Scanner;
public class Main
{
static long
euler(long n)
{
long result = n;
for(int i = 2;
i <= Math.sqrt(n);i++)
{
if (n % i ==
0) result -= result / i;
while (n % i ==
0) n /= i;
}
if (n >
1) result -= result / n;
return result;
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
while(con.hasNext())
{
long n = con.nextLong();
long sq = (long)Math.sqrt(n);
long res = (sq * sq == n) ? -sq * euler(sq) :
0;
for(long i = 1;
i <= sq; i++)
if (n % i ==
0)
res = res + i * euler(n/i) + (n / i) * euler(i);
System.out.println(res);
}
con.close();
}
}